Adjazenzlisten-Modell
In der Graphentheorie sind Adjazenzlisten, auch Nachbarschaftslisten genannt, eine Möglichkeit, Graphen zu repräsentieren. Dabei wird für jeden Knoten eine Liste, die Adjazenzliste, aller seiner Nachbarn (in ungerichteten Graphen) beziehungsweise Nachfolger (in gerichteten Graphen) angegeben. Betrachten wir den folgenden Graphen:
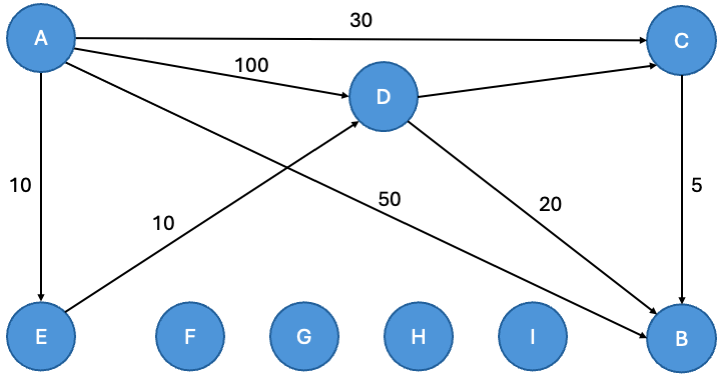
Der Beispielgraph ist gerichtet, wie an den Pfeilen, welche die Kanten zieren, leicht zu erkennen ist. Nicht alle Knoten sind verbunden. An den Kanten sind Gewichte notiert. Grundsätzlich könnten auch mehrere Gewichte mit unterschiedlicher Semantik angegeben sein. Uns reicht hier ein Gewicht. – Wir werden dieses daher auch direkt in der Adjazenzliste notieren und keine diesbezügliche Normalisierung vornehmen.
>In SQL speichern wir die Knoten in einer Tabelle. Hier soll das die Tabelle knoten sein. Die Adjazenzliste, die den Graphen modelliert, nennen wir hier graph. Weil wir nur jeweils ein Gewicht pro Kante betrachten wollen, schreiben wir dieses direkt mit in die Tabelle.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
CREATE TABLE knoten ( knoten_id INTEGER PRIMARY KEY, knoten CHAR(1) NOT NULL ); CREATE TABLE graph ( von_id INTEGER NOT NULL REFERENCES knoten (knoten_id), nach_id INTEGER NOT NULL REFERENCES knoten (knoten_id), kosten INTEGER NOT NULL, PRIMARY KEY (von_id, nach_id), CHECK ( von_id != nach_id ) ); INSERT INTO knoten (knoten_id, knoten) VALUES (1, 'A'), (2, 'B'), (3, 'C'), (4, 'D'), (5, 'E'), (6, 'F'), (7, 'G'), (8, 'H'), (9, 'I'); INSERT INTO graph (von_id, nach_id, kosten) VALUES (1, 2, 50), (1, 3, 30), (1, 4, 100), (1, 5, 10), (3, 2, 5), (4, 2, 20), (4, 3, 50), (5, 4, 10); |
Beachten Sie, dass wir es untersagt haben, Kanten zuzulassen, über die sich ein Knoten selbst referenziert. Grundsätzlich sind solche Kanten zulässig. Wir gehen hier jedoch implizit davon aus, dass jeder Knoten sich selbst erreichen kann. Die dabei entstehenden Kosten sind dann 0. Allerdings interessieren uns diese im Weiteren nicht. Auch in der Praxis macht eine explizite Betrachtung dieses Sachverhalts nur selten Sinn.
Eigenschaften von Graphen
Alle Kanten eines Graphen
Kanten sind die Verbindungen zwischen zwei unmittelbar verbundenen Knoten eines Graphen. Ist E eine Kante, dargestellt durch das Knotenpaar (n0, n1), dann ist n1 von n0 mit einer einfachen Traverse direkt erreichbar.
Die Fragestellung, alle Kanten eines Graphen auszugeben, ist trivial. Die Kanten entsprechen den in der Adjazenzliste, der Tabelle graph, abgelegten Datensätzen.
|
1 2 3 4 5 6 7 8 9 |
CREATE VIEW alle_kanten(von_id, nach_id) AS SELECT von_id , nach_id FROM graph ORDER BY von_id , nach_id; |
PostgreSQL gestattet es, Sichten zu sortieren. Das ist ein Feature, welches nicht jedes Datenbankmanagementsystem unterstützt. Auf die Verknüpfung mit der Knotentabelle habe ich verzichtet. Die kann, wenn gewünscht, ergänzt werden oder auch im Nachhinein in Verbindung mit der Abfrage der implementierten Sicht erfolgen.
+------+-------+ |von_id|nach_id| +------+-------+ |1 |2 | |1 |3 | |1 |4 | |1 |5 | |3 |2 | |4 |2 | |4 |3 | |5 |4 | +------+-------+
Alle verbundenen Knoten eines Graphen
Verbundene Knoten sind all die Knoten, die über Kanten in Beziehung stehen.
|
1 2 3 4 5 6 7 8 9 10 11 |
CREATE VIEW alle_verbundenen_knoten(knoten_id) AS SELECT von_id AS knoten_id FROM graph UNION SELECT nach_id FROM graph ORDER BY knoten_id; |
UNION sorgt dafür, Knoten, die sowohl Ausgangs- als auch Eingangsknoten sind, nicht mehrfach auszugeben.
+---------+ |knoten_id| +---------+ |1 | |2 | |3 | |4 | |5 | +---------+
Endpunkte von Pfaden
Pfadendpunkte sind die Start- und Endknoten eines Pfades. Dabei werden unterschiedliche Pfade mit gleichen Start- und Endknoten, wie beispielsweise A-B und A-C-B, zusammenfasst zu (A, B).
Zur Traversierung des Graphen nutzen wir einen rekursiven CTE (Common Table Expression).
In der Ankerabfrage ermitteln wir die Kanten eines Graphen. Die Rekursionsabfrage sucht dann, anhand des originären Graphen, nach Anschlusskanten zu den bereits ermittelten Kanten. Wir merken uns jeweils den alten Start- und neuen Endknoten eines so ermittelten Pfades.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
CREATE VIEW pfad_enpunkte(von_id, nach_id) AS WITH RECURSIVE pfade(von_id, nach_id) AS ( -- die originär bekannten Kanten bilden -- die Ausgangsbasis ... SELECT von_id , nach_id FROM graph UNION -- ... und werden um eventuelle Anschlusskanten -- ergänzt. SELECT p.von_id -- Startknoten merken , g.nach_id -- neuer Endknoten FROM graph g JOIN pfade p ON p.nach_id = g.von_id ) SELECT * FROM pfade ORDER BY von_id , nach_id; |
Die Abfrage setzte einen zyklenfreien Graphen voraus! – Andernfalls würde die Abfrage eine endlose Rekursion auslösen. Wir finden die folgenden Kontenpaare, welche die möglichen Pfade beschreiben:
- (1, 2), 1, 3), (1, 4), 1, 5),
- (3, 2),
- (4, 2), (4, 3),
- (5, 2), (5, 3) und (5, 4).
Hinweis: Die Anzahl der Endpunktpaare ist größer oder gleich der Anzahl der Kanten ei-nes Graphen. Sie ist kleiner oder gleich der Anzahl der Pfade eines Graphen.
Ein- und Ausgangsgrade
Der Eingangsgrad eines Knoten n ist die Anzahl verschiedener Kanten, die in n münden.
|
1 2 3 4 5 6 7 8 9 10 11 |
CREATE VIEW eingangsgrade(knoten_id, eingangsgrad) AS SELECT k.knoten_id , count(g.nach_id) AS eingangsgrad FROM knoten k LEFT JOIN graph g ON k.knoten_id = g.nach_id GROUP BY k.knoten_id ORDER BY k.knoten_id; |
Bei der Implementierung werden alle Knoten einbezogen, nicht nur die der Adjazenzliste. Es kann Knoten geben, und die gibt es im Beispielgraphen auch, deren Eingangsgrad 0 ist. Wir verwenden daher einen Outer-Join.
+---------+------------+ |knoten_id|eingangsgrad| +---------+------------+ |1 |0 | |2 |3 | |3 |2 | |4 |2 | |5 |1 | |6 |0 | |7 |0 | |8 |0 | |9 |0 | +---------+------------+
Analoges gilt für die Ausgangsgrade der Knoten. Der Ausgangsgrad eines Knotens n entspricht der Anzahl distinkter Kanten, die in n ihren Ursprung haben.
|
1 2 3 4 5 6 7 8 9 |
CREATE VIEW ausgangsgrade(knoten_id, ausgangsgrad) AS SELECT k.knoten_id , count(g.von_id) AS ausgangsgrad FROM knoten k LEFT JOIN graph g ON k.knoten_id = g.von_id GROUP BY k.knoten_id ORDER BY k.knoten_id; |
+---------+------------+ |knoten_id|ausgangsgrad| +---------+------------+ |1 |4 | |2 |0 | |3 |1 | |4 |2 | |5 |1 | |6 |0 | |7 |0 | |8 |0 | |9 |0 | +---------+------------+
Quelle, Senken, isolierte und interne Knoten
Ein Quellknoten hat einen positiven Ausgangsgrad und einen Eingangsgrad von 0, besitzt also nur von ihm ausgehende Kanten.
|
1 2 3 4 5 6 7 8 9 |
CREATE VIEW quellknoten(knoten_id) AS SELECT k.knoten_id FROM knoten k JOIN ausgangsgrade a ON k.knoten_id = a.knoten_id JOIN eingangsgrade e ON k.knoten_id = e.knoten_id WHERE ausgangsgrad > 0 AND eingangsgrad = 0; |
Im Beispielgraphen gibt es lediglich einen Quellknoten, den Knoten mit der ID 1.
Senken sind Knoten, die einen positiven Eingangsgrad und einen Ausgangsgrad von 0 haben, die also lediglich in sie eingehende Kanten aufweisen.
|
1 2 3 4 5 6 7 8 9 |
CREATE VIEW senken(knoten_id) AS SELECT k.knoten_id FROM knoten k JOIN eingangsgrade e ON k.knoten_id = e.knoten_id JOIN ausgangsgrade a ON k.knoten_id = a.knoten_id WHERE eingangsgrad > 0 AND ausgangsgrad = 0; |
Im Beispielgraphen existiert lediglich eine Senke, der Knoten mit der ID 2.
Interne Knoten sind Knoten, die sowohl einen positiven Eingangsgrad als auch einen positiven Ausgangsgrad besitzen.
|
1 2 3 4 5 6 7 8 9 |
CREATE VIEW interne_knoten(knoten_id) AS SELECT k.knoten_id FROM knoten k JOIN eingangsgrade e ON k.knoten_id = e.knoten_id JOIN ausgangsgrade a ON k.knoten_id = a.knoten_id WHERE eingangsgrad > 0 AND ausgangsgrad > 0; |
Interne Knoten sind:
+---------+ |knoten_id| +---------+ |3 | |4 | |5 | +---------+
Bei einem isolierten Knoten ist sowohl der Eingangs- als auch der Ausgangsgrad 0. Wir können auch sagen, isolierte Knoten sind nicht in der Menge der verbundenen Knoten enthalten. Ich beziehe mich bei meiner folgenden Abfrage auf die Ein- und Ausgangsgrade.
|
1 2 3 4 5 6 7 8 9 |
CREATE VIEW isolierte_knoten(knoten_id) AS SELECT k.knoten_id FROM knoten k JOIN eingangsgrade e ON k.knoten_id = e.knoten_id JOIN ausgangsgrade a ON k.knoten_id = a.knoten_id WHERE eingangsgrad = 0 AND ausgangsgrad = 0; |
Isolierte Knoten im Beispielgraphen sind die Knoten mit den IDs 6, 7, 8 und 9.
Grundlegende Operationen auf Graphen
Pfade und Pfadlängen
Das Suchen und Finden von Pfaden innerhalb eines Graphen sind die wichtigsten Operationen in Anwendungen, die auf Graphen basieren. Das sind beispielsweise Anwendungen aus den Bereichen Logistik, Stromversorgung, Workflow und ähnlichem mehr. Jedem bekannt sind sicherlich Navigationssysteme, die Wegstrecken zwischen zwei Orten A und B ermitteln.
Dabei spielt das Enumerieren der Pfade, also das Aufzählen aller in einem Pfad befindlichen Knoten, in der Reihenfolge ihrer Traversierung, eine wichtige Rolle. Wir nennen das Pfadenumeration.
Ein Pfad P der Länge L von Knoten n0 zu Knoten nk ist definiert als die Traverse von (L+1) direkt aufeinander folgender Knoten einer Sequenz von Kanten, wobei der erste Knoten mit 0 und der letzte Knoten mit k nummeriert ist. L entspricht also der Anzahl der Kanten eines Pfades.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
CREATE VIEW enumerierte_pfade(von_id, nach_id, pfad, laenge) AS WITH RECURSIVE pfade (von_id, nach_id, pfad, laenge) AS ( -- Ausgangsbasis sind die im Graphen hinterlegten Kanten. -- Jede dieser Kanten hat eine Länge von 1. SELECT von_id , nach_id , von_id || ',' || nach_id AS pfad , 1 AS laenge FROM graph UNION ALL -- Suchen von Anschlusskanten. Wird eine Anschlusskante -- gefunden, wird deren Endknoten an den Pfad der vorigen -- Kante angefügt. Die Länge des Pfades wird um den Wert -- 1 erhöht. SELECT p.von_id , g.nach_id , p.pfad || ',' || g.nach_id , laenge + 1 FROM graph g JOIN pfade p ON p.nach_id = g.von_id ) SELECT von_id , nach_id , pfad , laenge FROM pfade ORDER BY von_id , nach_id; |
Wir nutzen, analog zur Bestimmung der Pfadendpunkte, einen rekursiven CTE. Allerdings ist die Rekursionsabfrage dahingehend zu modifizieren, jetzt mit UNION ALL statt lediglich UNION eingeleitet zu werden. Da sich die Pfade alle voneinander unterscheiden, ist eine Komprimierung von Dubletten, die es nicht gibt, sinnlos und würde lediglich für Ineffizienz sorgen. Ansonsten merken wir uns wiederum den Startknoten eines Pfades und ergänzen den Pfad um den Endknoten einer gefundenen Anschlusskante. Zusätzlich protokollieren wir die Entwicklung eines jeden Pfades und schreiben dessen Länge fort. Mit jeder zusätzlich gefundenen Kante erhöht sich die Länge eines Pfades um 1.
+------+-------+---------+------+ |von_id|nach_id|pfad |laenge| +------+-------+---------+------+ |1 |2 |1,2 |1 | |1 |3 |1,3 |1 | |1 |4 |1,4 |1 | |1 |5 |1,5 |1 | |3 |2 |1,5,4,3,2|4 | |3 |2 |3,2 |1 | |3 |2 |4,3,2 |2 | |3 |2 |1,3,2 |2 | |3 |2 |5,4,3,2 |3 | |3 |2 |1,4,3,2 |3 | |4 |2 |5,4,2 |2 | |4 |2 |1,4,2 |2 | |4 |2 |4,2 |1 | |4 |2 |1,5,4,2 |3 | |4 |3 |1,5,4,3 |3 | |4 |3 |4,3 |1 | |4 |3 |5,4,3 |2 | |4 |3 |1,4,3 |2 | |5 |4 |1,5,4 |2 | |5 |4 |5,4 |1 | +------+-------+---------+------+
In unserem Beispielgraphen finden wir 20 verschiedene Pfade vor, die wir traversieren können.
Kürzeste Pfade
Der kürzeste Pfad zwischen zwei Knoten ist der Pfad mit der geringsten Länge, also der geringsten Anzahl zu traversierenden Kanten.
Zur Ermittlung der kürzesten Pfade benötigen wir sämtliche Pfade und deren Längen. Für jeden Pfad, gekennzeichnet durch seinen jeweiligen Start- und Endknoten, ist dann der Pfad zu wählen, dessen Länge minimal ist.
Wir nutzen die bereits ermittelten Pfade aus der Sicht enumerierte_pfade und deren Längen in einem neu zu erstellenden CTE. Wir nennen diese Teilabfrage pfade. Für die Ermittlung der kürzesten Verbindungen zwischen zwei Endpunkten von Pfaden, die zwar verschieden sind, jedoch gleiche Start- und Endknoten aufweisen, beziehen wir uns auf die Teilabfrage pfade. Das hat den Vorteil, die Sicht enumerierte_pfade nur einmalig auszuführen. Würden wir uns stattdessen nochmals explizit auf enumerierte_pfade beziehen, würde die Sicht doppelt ausgeführt. – Es ist ein großer Effizienzvorteil von CTEs, eine Abfrage nur einmalig ausführen zu müssen, sich aber dennoch mehrfach auf ein solches Ergebnis beziehen zu können.
Sobald wir sowohl die vollständigen Pfade als auch die kürzesten Verbindungen, gekennzeichnet durch ihre jeweiligen Start- und Endknoten sowie die Länge eines solchen Pfades ermittelt haben, können wir die Teilergebnisse zusammenfassen. Dazu verknüpfen wir sie anhand der Start- und Endknoten sowie der Pfadlänge.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
CREATE VIEW kuerzeste_pfade(von_id, nach_id, pfad, laenge) AS WITH pfade (von_id, nach_id, pfad, laenge) AS ( -- Alle Pfade mit Pfadlängen SELECT * FROM enumerierte_pfade ) , kuerzeste(von_id, nach_id, laenge) AS ( -- minimale Längen zwischen zwei Endpunkten -- eines Pfades ermitteln SELECT von_id , nach_id , min(laenge) FROM pfade GROUP BY von_id , nach_id ) -- Synthese der insgesamt ermittelten Pfade mit den -- jeweils ermittelten kleinsten Längen zwischen den -- Start- und Endknoten SELECT p.von_id , p.nach_id , p.pfad , p.laenge FROM pfade p JOIN kuerzeste k ON p.von_id = k.von_id AND p.nach_id = k.nach_id AND p.laenge = k.laenge ORDER BY p.von_id , p.nach_id; |
+------+-------+-----+------+ |von_id|nach_id|pfad |laenge| +------+-------+-----+------+ |1 |2 |1,2 |1 | |1 |3 |1,3 |1 | |1 |4 |1,4 |1 | |1 |5 |1,5 |1 | |3 |2 |3,2 |1 | |4 |2 |4,2 |1 | |4 |3 |4,3 |1 | |5 |2 |5,4,2|2 | |5 |3 |5,4,3|2 | |5 |4 |5,4 |1 | +------+-------+-----+------+
Kostenminimale Pfade
Die Ermittlung der kostenminimalen Pfade erfolgt analog zur Ermittlung der kürzesten Pfade. Wir verwenden lediglich die den Kanten zugewiesenen Gewichte statt die Pfadlängen zu inkrementieren.
Zuerst erstellen wir uns eine Sicht namens enumerierte_pfade_mit_kosten, die lediglich eine einfache Modifikation im genannten Sinne von enumerierte_pfade ist.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
CREATE VIEW enumerierte_pfade_mit_kosten(von_id, nach_id, pfad, kosten) AS WITH RECURSIVE pfade (von_id, nach_id, pfad, kosten) AS ( -- Ausgangsbasis sind die im Graphen hinterlegten Kanten. -- Jede dieser Kanten hat zu ihr angegebenen Basis-Kosten. SELECT von_id , nach_id , von_id || ',' || nach_id AS pfad , kosten FROM graph UNION ALL -- Suchen von Anschlusskanten. Wird eine Anschlusskante -- gefunden, wird deren Endknoten an den Pfad der vorigen -- Kante angefügt. Die Kosten des Pfades werden um den Wert -- der Kosten der zusätzlichen Kante inkrementiert. SELECT p.von_id , g.nach_id , p.pfad || ',' || g.nach_id , g.kosten + p.kosten FROM graph g JOIN pfade p ON p.nach_id = g.von_id ) SELECT von_id , nach_id , pfad , kosten FROM pfade ORDER BY von_id , nach_id; |
+------+-------+---------+------+ |von_id|nach_id|pfad |kosten| +------+-------+---------+------+ |1 |2 |1,2 |50 | |1 |2 |1,3,2 |35 | |1 |2 |1,4,2 |120 | |1 |2 |1,4,3,2 |155 | |1 |2 |1,5,4,2 |40 | |1 |2 |1,5,4,3,2|75 | |1 |3 |1,5,4,3 |70 | |1 |3 |1,3 |30 | |1 |3 |1,4,3 |150 | |1 |4 |1,5,4 |20 | |1 |4 |1,4 |100 | |1 |5 |1,5 |10 | |3 |2 |3,2 |5 | |4 |2 |4,2 |20 | |4 |2 |4,3,2 |55 | |4 |3 |4,3 |50 | |5 |2 |5,4,2 |30 | |5 |2 |5,4,3,2 |65 | |5 |3 |5,4,3 |60 | |5 |4 |5,4 |10 | +------+-------+---------+------+
Natürlich stimmt die Anzahl der so ermittelten Pfade mit der Anzahl überein, die wir mit der Sicht enumerierte_pfade ermittelt haben. Es gibt 20 verschiedene Pfade.
Mit der Bestimmung der minimalen Kosten verfahren wir ebenso wie bereits gehabt.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
CREATE VIEW minimale_kosten(von_id, nach_id, pfad, kosten) AS WITH pfade (von_id, nach_id, pfad, kosten) AS ( -- Alle Pfade mit Kosten SELECT * FROM enumerierte_pfade_mit_kosten ) , minimale_kosten(von_id, nach_id, kosten) AS ( -- minimale Kosten zwischen zwei Endpunkten -- eines Pfades ermitteln SELECT von_id , nach_id , min(kosten) FROM pfade GROUP BY von_id , nach_id ) -- Synthese der insgesamt ermittelten Pfade mit den -- jeweils ermittelten geringsten Kosten zwischen den -- Start- und Endknoten SELECT p.von_id , p.nach_id , p.pfad , p.kosten FROM pfade p JOIN minimale_kosten k ON p.von_id = k.von_id AND p.nach_id = k.nach_id AND p.kosten = k.kosten ORDER BY p.von_id , p.nach_id; |
Die Anzahl der kostenminimalen Pfade kann von den kürzesten Pfaden abweichen. In unserem Beispielgraphen ist die Anzahl der Pfade jedoch gleich.
+------+-------+-----+------+ |von_id|nach_id|pfad |kosten| +------+-------+-----+------+ |1 |2 |1,3,2|35 | |1 |3 |1,3 |30 | |1 |4 |1,5,4|20 | |1 |5 |1,5 |10 | |3 |2 |3,2 |5 | |4 |2 |4,2 |20 | |4 |3 |4,3 |50 | |5 |2 |5,4,2|30 | |5 |3 |5,4,3|60 | |5 |4 |5,4 |10 | +------+-------+-----+------+
Vergleichen Sie die Pfade, so erkennen Sie, dass die kürzesten Pfade nicht zwingend auch die kostengünstigsten sein müssen und umgekehrt. Von Knoten 1 zu Knoten 2, von A nach B, ist die direkte Verbindung der kürzeste Pfad. Die kostengünstigste Traverse ist jedoch A-C-B.
Zyklenerkennung
Die bisher besprochenen Abfragen, so sie rekursiv formuliert waren, setzen azyklische Graphen voraus. Nun können Graphen aber auch zyklisch sein. Streckennetze, Stadtpläne usw. sind typische Beispiele, in welchen mehr oder minder garantiert Zyklen vorhanden sind. Verwenden wir die bisherigen Rekursionsabfragen, die nicht in der Lage sind, einen Zyklus zu erkennen, terminieren sie nicht. – Am Ende terminieren sie schon, jedoch nur, weil die maximal zulässige Rekursionstiefe überschritten wird und das Datenbankmanagementsystem einen diesbezüglichen Fehler wirft.
Wollen wir in der Lage sein, auch zyklische Graphen zu verarbeiten, müssen wir in der Lage sein, Zyklen zu erkennen und eine Verarbeitung abzubrechen, sobald wir einen Zyklus erkennen.
Die bereits besprochene Pfadenumeration bildet die Basis für die Erkennung von Zyklen. Wird eine bereits im Pfad vorhandene Kante nochmals durchlaufen, haben wir einen Zyklus entdeckt. In diesem Fall ist die Verarbeitung abzubrechen. Um dies zu zeigen, werden wir zwei Dinge unternehmen:
- Wir fügen eine weitere Kante in unseren Beispielgraphen ein. Diese neue Kante manifestiert mindestens einen Zyklus.
- Wir werden die Pfadenumeration ergänzen. Bislang haben wir dazu lediglich eine Zeichenkette für die Ausgabe verwendet, um die traversierten Knoten in der korrekten Reihenfolge ausgeben zu können. Wir benötigen jedoch die durchlaufenen Kanten. PostgreSQL unterstützt Arrays. Mit ihrer Hilfe können wir jede durchlaufe-ne Kante in einem Array-Element das Datensatz (ROW) ablegen. So können wir leicht prüfen, ob eine in der Rekursion anzufügende Kante bereits im Pfad vorhanden ist.
Dies ist der Beispielgraph mit der zusätzlich eingefügten Kante:
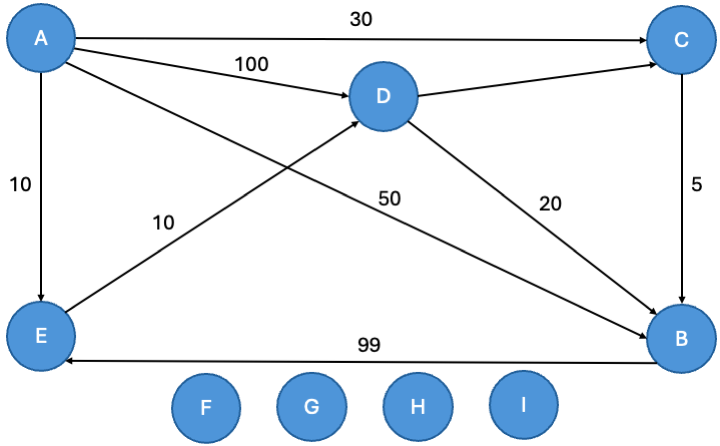
Fügen wir die zusätzlich eingefügte Kante in die Adjazenzliste, Tabelle graph, ein und erzeigen so den oben gezeigten zyklischen Graphen:
|
1 2 3 |
INSERT INTO graph (von_id, nach_id, kosten) VALUES (2, 5, 99); |
Jeder Pfad, der den Knoten B, ID 2, enthält, wird durch diese Maßnahme potenziell zyklisch. Ein Zyklus liegt dann vor, wenn eine bereits traversierte Kante nochmals durchlaufen werden soll. Versuchen wir eine unserer bisherigen rekursiven Abfragen auszuführen, geschieht genau das und die Abfrage schlägt fehl. Wir modifizieren bzw. ergänzen daher die Pfadenumeration, so wie oben angesprochen, und etablieren eine Zykluserkennung.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
CREATE VIEW enumerierte_pfade_mit_zykluserkennung(von_id, nach_id, pfad, laenge, ist_zyklisch) AS WITH RECURSIVE pfade (von_id, nach_id, pfad, laenge, kanten, ist_zyklisch) AS ( SELECT von_id , nach_id , von_id || ',' || nach_id AS pfad , 1 AS laenge -- erste Kante eines Pfades , ARRAY [ROW (von_id, nach_id)] AS kanten -- noch kein Zyklus , FALSE AS ist_zyklisch FROM graph UNION ALL SELECT p.von_id , g.nach_id , p.pfad || ',' || g.nach_id , laenge + 1 -- Kanten-Array fortschreiben , p.kanten || ROW (p.von_id, g.nach_id) -- prüfen, ob neue Kante bereits vorhanden - wenn ja -> Zyklus , ROW (p.von_id, g.nach_id) = ANY (p.kanten) FROM graph g JOIN pfade p ON p.nach_id = g.von_id -- bei Zyklus aktuelle Pfadentwicklung abbrechen WHERE NOT ist_zyklisch ) SELECT von_id , nach_id , pfad , laenge , ist_zyklisch FROM pfade ORDER BY pfad; |
Die Zeichenkettenverknüpfung für die Ausgabe der Pfade behalten wir bei. Wir spendieren uns aber ein Array namens kanten. Darin protokollieren wir die durchlaufenen Kanten in Form von Datensätzen, bestehend aus dem Start- und Endknoten einer Kante. Ein solches Array von Strukturen kann von Sichten nicht als Ausgabefeld zurückgegeben werden, weshalb wir es nur intern nutzen. In der Ankerabfrage mit der jeweils ersten Kante eines Pfades initialisiert, schreiben wir jedes Kanten-Array in der Rekursionsabfrage fort. Ist eine angefügte Kante bereits im Array enthalten, haben wir einen Zyklus entdeckt.
Bei PostgreSQL müssen wir die Zykluserkennung nicht selbst implementieren. PostgreSQL bietet eine CYCLE-Klausel, die das für uns übernimmt. Laut PostgreSQL-Dokumentation arbeitet die Klausel so, wie ich das im Rahmen der manuellen Zyklenerkennung vorgestellt habe. Bequemer ist es jedoch, die in PostgreSQL vorhandene CYCLE-Klausel zu nutzen.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
CREATE VIEW enumerierte_pfade_mit_zykluserkennung (von_id, nach_id, pfad, laenge, ist_zyklisch) AS WITH RECURSIVE pfade (von_id, nach_id, pfad, laenge) AS ( SELECT von_id , nach_id , von_id || ',' || nach_id AS pfad , 1 AS laenge FROM graph UNION ALL SELECT p.von_id , g.nach_id , p.pfad || ',' || g.nach_id , laenge + 1 FROM graph g JOIN pfade p ON p.nach_id = g.von_id ) CYCLE von_id, nach_id SET ist_zyklisch USING pfad_enum SELECT von_id , nach_id , pfad , laenge , ist_zyklisch FROM pfade ORDER BY pfad; |
Hinter der CYCLE-Klausel werden die zu überwachenden Attribute als Liste notiert. SET definiert ein virtuelles Feld für die Überwachung, welches in der Ergebnisabfrage genutzt werden kann. Analoges gilt für pfad_enum, dem hinter USING anzugebenden Bezeichner. pfad_enum ist ein Array von Strukturen. Es entspricht dem Kanten-Array, welches wir vorher selbst konstruiert haben.
Ich möchte nochmals kurz auf den Begriff „Zyklus“ eingehen, um eventuelle Missverständnisse zu vermeiden. Eine Rundreise von Knoten B (2) über E (5), D (4) und wieder zu B (2) stellt noch keinen Zyklus dar. Wir sind zwar umgangssprachlich einmal im Kreis gegangen, haben aber keine Kante mehrfach traversiert. Wenn Sie derartige Rundreisen unterbinden wollen, müssen Sie zusätzlich verlangen, das Start- und Endknoten eines Pfades verschieden sind. Diese Bedingung ist jedoch umgekehrt, zur Vermeidung von Zyklen nicht hinreichend. Der Pfad A (1), B (2), E (5), D (4), B (2) ist nämlich, um nur ein Beispiel herauszugreifen, zyklisch. Start- und Endknoten des Pfades sind aber verschieden.
Egal, ob Sie mit oder ohne CYCLE-Klausel arbeiten wollen, die sich ergebenden Pfade aus unserem zyklischen Beispielgraphen lauten wie folgt:
+------+-------+---------+------+------------+ |von_id|nach_id|pfad |laenge|ist_zyklisch| +------+-------+---------+------+------------+ |1 |2 |1,2 |1 |false | |1 |5 |1,2,5 |2 |false | |1 |4 |1,2,5,4 |3 |false | |1 |3 |1,2,5,4,3|4 |false | |1 |3 |1,3 |1 |false | |1 |2 |1,3,2 |2 |false | |1 |5 |1,3,2,5 |3 |false | |1 |4 |1,3,2,5,4|4 |false | |1 |4 |1,4 |1 |false | |1 |2 |1,4,2 |2 |false | |1 |5 |1,4,2,5 |3 |false | |1 |3 |1,4,3 |2 |false | |1 |2 |1,4,3,2 |3 |false | |1 |5 |1,4,3,2,5|4 |false | |1 |5 |1,5 |1 |false | |1 |4 |1,5,4 |2 |false | |1 |2 |1,5,4,2 |3 |false | |1 |3 |1,5,4,3 |3 |false | |1 |2 |1,5,4,3,2|4 |false | |2 |5 |2,5 |1 |false | |2 |4 |2,5,4 |2 |false | |2 |2 |2,5,4,2 |3 |false | |2 |3 |2,5,4,3 |3 |false | |2 |2 |2,5,4,3,2|4 |false | |3 |2 |3,2 |1 |false | |3 |5 |3,2,5 |2 |false | |3 |4 |3,2,5,4 |3 |false | |3 |3 |3,2,5,4,3|4 |false | |4 |2 |4,2 |1 |false | |4 |5 |4,2,5 |2 |false | |4 |4 |4,2,5,4 |3 |false | |4 |3 |4,2,5,4,3|4 |false | |4 |3 |4,3 |1 |false | |4 |2 |4,3,2 |2 |false | |4 |5 |4,3,2,5 |3 |false | |4 |4 |4,3,2,5,4|4 |false | |5 |4 |5,4 |1 |false | |5 |2 |5,4,2 |2 |false | |5 |5 |5,4,2,5 |3 |false | |5 |3 |5,4,3 |2 |false | |5 |2 |5,4,3,2 |3 |false | |5 |5 |5,4,3,2,5|4 |false | +------+-------+---------+------+------------+
Zusätzlich, zu diesen 42 Pfaden, existieren 18 zyklische Pfade.